ЭС: А.Н.Колмогоров

КОЛМОГОРОВ АНДРЕЙ НИКОЛАЕВИЧ (12(25).04.1903, Тамбов – 20.10.1987, Москва), математик.

 

Окончил физико-математический факультет МГУ (1925). Ученик Н.Н. Лузина.

Доктор физико-математических наук (1935). Профессор (1931).

Академик отделения физико-математических наук (математика) АН СССР (1939).

Академик АПН РСФСР (1965). Академик отделения дидактики и частных методик АПН СССР (1968).

 

Декан (1954–1958); заведующий кафедрой математической логики (1980–1987); заведующий кафедрой математической статистики (1976–1980); заведующий кафедрой теории вероятностей (1935–1965); заведующий кафедрой общего математического анализа (1933–1935) механико-математического факультета. Заведующий межфакультетской лабораторией вероятностных и статистических методов (1966–1976). Директор Института математики (1935–1939).

 

Научная и педагогическая деятельность. В сфере научных интересов тригонометрические ряды, теория меры, теория множеств, теория интеграла, теория функций, теория вероятностей. Командирован с научной целью в Германию и Францию (1930–1931).

Один из крупнейших математиков XX в. В студенческие годы, исследуя ряды Фурье, он впервые построил пример интегрируемой по Лебегу функции на отрезке [0,2π], ряд Фурье которой расходится почти всюду, ставший одним из самых замечательных достижений в теории тригонометрических рядов (1922).

Основополагающее значение имеют его работы в области теории вероятностей, начало которым положила статья «О сходимости рядов, члены которых определяются случаем», написанная им совместно с А.Я. Хинчиным (1924). Важную роль в развитии теории вероятностей, расширении областей её приложений сыграла фундаментальная монография «Основные понятия теории вероятностей» (1933). А.Н. Колмогорову удалось практически завершить исследования Я. Бернулли, П.Л. Чебышёва и А.А. Маркова по отысканию достаточных (а также необходимых и достаточных) условий справедливости закона больших чисел и усиленного закона больших чисел. Он построил аксиоматику теории вероятностей и заложил основы теории марковских случайных процессов с непрерывным временем, связал теорию вероятностей в целом с теорией дифференциальных уравнений с частными производными и математической физикой. Эти исследования послужили развитию стохастических дифференциальных уравнений и стохастического анализа.

Совместно с А.М. Обуховым создал целостную теорию локально-изотропной турбулентности. Существенно дополнил представление о каскадном процессе передачи энергии, отметив ослабление ориентирующего влияния среднего течения при каждом переходе к более мелким структурам, и, исходя из этого, сформулировал гипотезу о том, что статистический режим достаточно мелкомасштабной турбулентности, является универсальным и определяется лишь двумя размерными параметрами – средней скоростью диссипации энергии и коэффициентом вязкости. (1941, «Локальная структура турбулентности в несжимаемой жидкости при очень больших числах Рейнольдса»; 1942, «Уравнения турбулентного движения несжимаемой жидкости»).

В области топологии ввёл верхний граничный оператор и понятие когомологии ‒ важнейшее понятие топологии и её приложений. Сформулировал идею топологического векторного пространства.

 

А.Н. Колмогоров внёс значительный вклад в общую теорию гамильтоновых систем, теорию информации, эргодическую теорию динамических систем (1950-е гг.). Доказанная им теорема о сохранении инвариантных торов при малом аналитическом возмущении вполне интегрируемой гамильтоновой системы (1954), распространённая Ю. Мозером на случай гладких функций (1962), а также открытие В.И. Арнольдом универсального механизма неустойчивости в системах со многими степенями свободы, близких к интегрируемым (1964, диффузия Арнольда) легли в основу широко известной КАМ-теории – теории Колмогорова–Арнольда–Мозера, являющейся ветвью теории динамических систем, которая изучает малые возмущения почти периодической динамики в гамильтоновых системах и родственных им случаях. Наиболее известными примерами, относящимися к области применимости теории, являются вопросы об устойчивости Солнечной системы, об удержании плазмы в проектах контролируемой ядерной реакции и управлении ускорителями.

А.Н. Колмогорову и В.И. Арнольду принадлежит решение 13-й проблемы Гильберта (можно ли, в частности, решить общее уравнение седьмой степени с помощью функций, зависящих только от двух переменных?). При исследовании знаменитой проблемы А.Н. Колмогоров доказал, что функции четырёх переменных не существуют: любая непрерывная функция четырёх или большего числа переменных может быть сведена к непрерывным функциям трёх переменных. Он показал, что для сведения непрерывных функций трёх переменных к непрерывным функциям двух переменных достаточно найти универсальное дерево, любая непрерывная функция на котором представима в виде суммы трёх непрерывных функций, каждая из которых зависит лишь от одной координаты. Эту задачу решил В.И. Арнольд.

 

Интересны работы А.Н. Колмогорова в области лингвистики и филологии, посвящённые анализу статистики речи и стиховедению (1943, «Замечания об основах русского стихосложения»). Применяя методы математической статистики и теории информации, он указал подходы к некоторым вопросам, чрезвычайно важным для понимания устройства языка. Он предположил, что «энтропию речи» (мера количества информации, передаваемой речью) можно разложить на две компоненты: внеречевую (смысловую, семантическую) и собственно речевую (лингвистическую) информацию. Первая из этих компонент характеризует разнообразие, позволяющее передавать различную смысловую информацию; вторая – «остаточная энтропия», характеризует разнообразие возможных способов выражения одной и той же или равносильной смысловой информации. Наличие «остаточной энтропии» обеспечивает возможность придания речи особой художественной выразительности при передаче задуманной смысловой информации. В 1960 г. он прочитал на механико-математическом факультете цикл из трёх двухчасовых докладов по математическим методам исследования русского стиха. А.Н. Колмогоров поддержал идею создания отделения теоретической и прикладной лингвистики на филологическом факультете (1960).

 

22 апреля 1964 г. А.Н. Колмогоров читает лекцию «Кибернетика в изучении Жизни и мышления» в Актовом зале Главного здания МГУ

В начале 1960-х гг. под руководством А.И. Маркушевича, возглавлявшего комиссию по содержанию образования в школах, созданную при президиумах АН СССР и АПН РСФСР/СССР, была начата знаменитая школьная реформа (министр просвещения СССР М.А. Прокофьев). Привлечённый к работе А.Н. Колмогоров руководил комиссией по математическому образованию, сформировавшей принципиально новую программу и авторские коллективы для написания соответствующих школьных учебников (1965–1980). Реформа встретила сильное сопротивление со стороны учительского сообщества, учащихся и их родителей. В 1978 г. при коллегии Министерства просвещения РСФСР была создана новая комиссия по подготовке программ и учебников по математике для 4–10 классов, научным руководителем которой стал А.Н. Тихонов.

 

 

1977 г. А.Н. Колмогоров с учащимися и преподавателями ФМШ

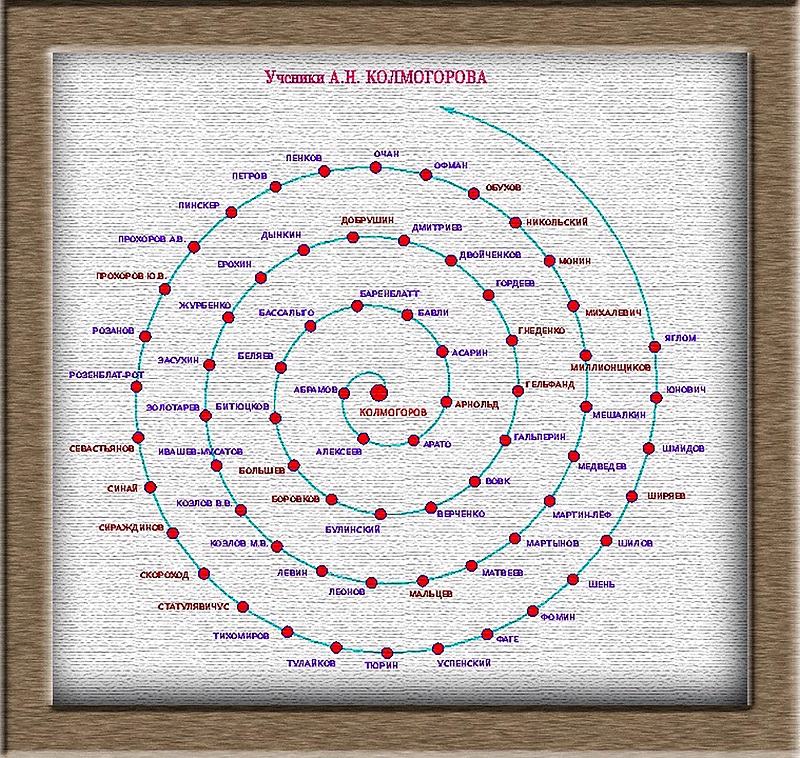
«Спираль» А.Н. Колмогорова

 

Великая Отечественная война. По заданию Главного артиллерийского управления Красной армии вместе с А.Я. Хинчиным выполнил исследования о наиболее выгодном рассеивании снарядов при стрельбе по площадям, что оказало серьёзную помощь в повышении эффективности артиллерийского огня.

 

Государственные награды: Герой Социалистического Труда (1963). Ордена – Ленина (1944, 1945, 1953, 1961, 1963, 1973, 1975), Трудового Красного Знамени (1940), Октябрьской Революции (1983), медаль «За доблестный труд в Великой Отечественной войне 1941–1945 гг.».

 

Награды иностранных государств: орден Трудового Красного Знамени/Munka Vörös Zásló Érdemrendje (Венгерская Народная Республика, 1975).

 

Основные труды: «Исследование уравнения диффузии, соединённой с возрастанием количества вещества и его применение к одной биологической проблеме» (1937), «Цепи Маркова со счётным числом возможных состояний» (1937), «Стационарные последовательности в гильбертовом пространстве» (1941), «Предельные распределения для сумм независимых случайных величин» (соавт., 1949), «О профессии математика» (1952), «Теория передачи информации» (1956), «Жизнь и мышление с точки зрения кибернетики» (1962), «Физико-математическая школа при МГУ» (соавт., 1981), учебники и учебные пособия «Введение в теорию функций действительного переменного» (соавт., 1933), «Введение в теорию множеств и теорию функций» (соавт., 1948), «Элементы теории функций и функционального анализа» (соавт., 1954), «Введение в анализ» (1966), «Введение в математическую логику» (соавт., 1982), «Математическая логика. Дополнительные главы» (соавт., 1984), «Введение в теорию вероятностей» (соавт., 1982).

 

 

Литература: Ширяев А.Н. (ред.-сост.) Колмогоров в воспоминаниях. – М., 1993; Успенский В.А. Колмогоров и филологические науки. Вестник Московского университета. 2009. Серия Филология. №6; Филинов Е.Н. Академик А.Н.Колмогоров. Виртуальный компьютерный музей; А.Н.Колмогоров. Математический институт им. В.А.Стеклова РАН.